Reprint from THE "HOW-TO-DO-IT" BOOKS

CARPENTRY FOR BOYS
By J. S. ZERBE, M.E.
Copyright, 1914, by
THE NEW YORK BOOK COMPANY

CHAPTER VIII

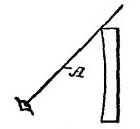
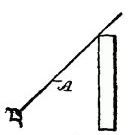
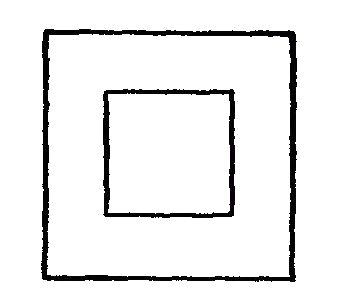
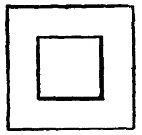
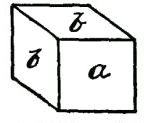
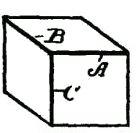
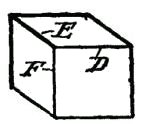
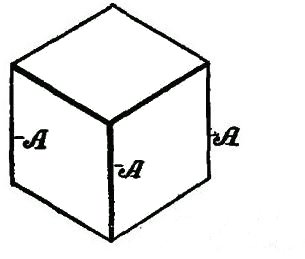
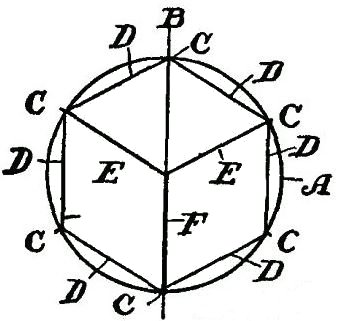
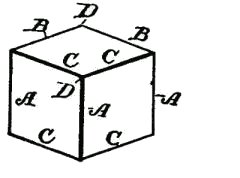
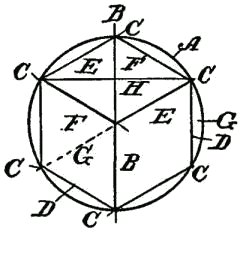
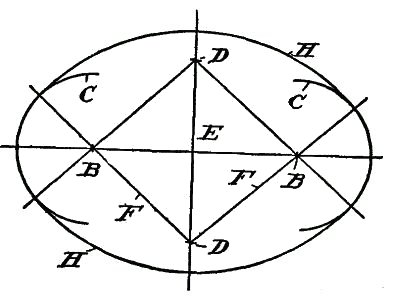
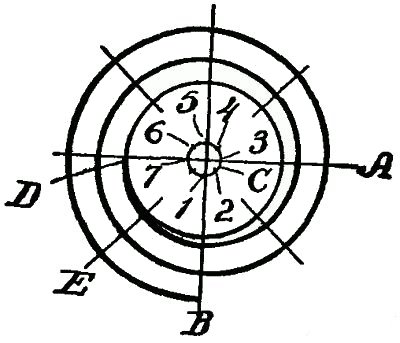
DRAWING AND ITS UTILITY

A knowledge of drawing, at least so far as the fundamentals are concerned, is of great service to the beginner. All work, after being conceived in the brain, should be transferred to paper. A habit of this kind becomes a pleasure, and, if carried out persistently, will prove a source of profit. The boy with a bow pen can easily draw circles, and with a drawing or ruling pen he can make straight lines.

Representing Objects.—But let him try to represent some object, and the pens become useless. There is a vast difference in the use of drawing tools and free-hand drawing. While the boy who is able to execute free-hand sketches may become the better artist, still that art would not be of much service to him as a carpenter. First, because the use of tools gives precision, and this is necessary to the builder; and, second, because the artist deals wholly with perspectives, whereas the builder must execute from plane surfaces or elevations.

Forming Lines and Shadows.—It is not my intention to furnish a complete treatise on this subject, but to do two things, one of which will be to show, among other features, how simple lines form objects; how shading becomes an effective aid; how proportions are formed; and, second, how to make irregular forms, and how they may readily be executed so that the boy may be able to grasp the ideas for all shapes and structural devices.

Analysis of Line Shading.—In the demonstration of this work I shall give an analysis of the simple lines formed, showing the terms used to designate the lines, curves, and formations, so that when any work is laid out the beginner will be able, with this glossary before him, to describe architecturally, as well as mathematically, the angles and curves with which he is working.

How to Characterize Surface.—Suppose we commence simply with straight lines. How shall we determine the character of the surface of the material between the two straight lines shown in Fig. 125? Is it flat, rounded, or concaved? Let us see how we may treat the surface by simple lines so as to indicate the configuration.

Concave Surfaces.—In Fig. 126 the shading lines commence at the upper margin, and are heaviest there, the lines gradually growing thinner and farther apart.

Convex Surfaces.—In Fig. 127 the shading is very light along the upper margin, and heavy at the lower margin. The first shaded figure, therefore, represents a concaved surface, and the second figure a convex surface. But why? Simply for the reason that in drawings, as well as in nature, light is projected downwardly, hence when a beam of light moves past the margin of an object, the contrast at the upper part, where the light is most intense, is strongest.

The shading of the S-shaped surface (Fig. 128) is a compound of Figs. 126 and 127.

Shadows From a Solid Body.—We can understand this better by examining Fig. 129, which shows a vertical board, and a beam of light (A) passing downwardly beyond the upper margin of the board. Under these conditions the upper margin of the board appears darker to the vision, by contrast, than the lower part. It should also be understood that, in general, the nearer the object the lighter it is, so that as the upper edge of the board is farthest from the eye the heavy shading there will at least give the appearance of distance to that edge.

But suppose that instead of having the surface of the board flat, it should be concaved, as in Fig. 130, it is obvious that the hollow, or the concaved, portion of the board must intensify the shadows or the darkness at the upper edge. This explains why the heavy shading in Fig. 126 is at that upper margin.

Flat Effects.—If the board is flat it may be shaded, as shown in Fig. 131, in which the lines are all of the same thickness, and are spaced farther and farther apart at regularly increasing intervals.

The Direction of Light.—Now, in drawing, we must observe another thing. Not only does the light always come from above, but it comes also from the left side. I show in Fig. 132 two squares, one within the other. All the lines are of the same thickness. Can you determine by means of such a drawing what the inner square represents? Is it a block, or raised surface, or is it a depression?

Raised Surfaces.—Fig. 133 shows it in the form of a block, simply by thickening the lower and the right-hand lines.

Depressed Surfaces.—If, by chance, you should make the upper and the left-hand lines heavy, as in Fig. 134, it would, undoubtedly, appear depressed, and would need no further explanation.

Full Shading,—But, in order to furnish an additional example of the effect of shading, suppose we shade the surface of the large square, as shown in Fig. 135, and you will at once see that not only is the effect emphasized, but it all the more clearly expresses what you want to show. In like manner, in Fig. 136, we shade only the space within the inner square, and it is only too obvious how shadows give us surface conformation.

Illustrating Cube Shading.—In Fig. 137 I show merely nine lines joined together, all lines being of equal thickness.

As thus drawn it may represent, for instance, a cube, or it may show simply a square base (A) with two sides (B, B) of equal dimensions.

Shading Effects.—Now, to examine it properly so as to observe what the draughtsman wishes to express, look at Fig. 138, in which the three diverging lines (A, B, C) are increased in thickness, and the cube appears plainly. On the other hand, in Fig. 139, the thickening of the lines (D, E, F) shows an entirely different structure.

It must be remembered, therefore, that to show raised surfaces the general direction is to shade heavily the lower horizontal and the right vertical lines. (See Fig. 133.)

Heavy Lines.—But there is an exception to this rule. See two examples (Fig. 140). Here two parallel lines appear close together to form the edge nearest the eye. In such cases the second, or upper, line is heaviest. On vertical lines, as in Fig. 141, the second line from the right is heaviest. These examples show plain geometrical lines, and those from Figs. 138 to 141, inclusive, are in perspective.

Perspective.—A perspective is a most deceptive figure, and a cube, for instance, may be drawn so that the various lines will differ in length, and also be equidistant from each other. Or all the lines may be of the same length and have the distances between them vary. Supposing we have two cubes, one located above the other, separated, say, two feet or more from each other. It is obvious that the lines of the two cubes will not be the same to a camera, because, if they were photographed, they would appear exactly as they are, so far as their positions are concerned, and not as they appear. But the cubes do appear to the eye as having six equal sides. The camera shows that they do not have six equal sides so far as measurement is concerned. You will see, therefore, that the position of the eye, relative to the cube, is what determines the angle, or the relative angles of all the lines.

A True Perspective of a Cube.—Fig. 142 shows a true perspective—that is, it is true from the measurement standpoint. It is what is called an isometrical view, or a figure in which all the lines not only are of equal length, but the parallel lines are all spaced apart the same distances from each other.

Isometric Cube.—I enclose this cube within a circle, as in Fig. 143. To form this cube the circle (A) is drawn and bisected with a vertical line (B). This forms the starting point for stepping off the six points (C) in the circle, using the dividers without resetting, after you have made the circle. Then connect each of the points (C) by straight lines (D). These lines are called chords. From the center draw two lines (E) at an angle and one line (F) vertically. These are the radial lines. You will see from the foregoing that the chords (D) form the outline of the cube—or the lines farthest from the eye, and the radial lines (E, F) are the nearest to the eye. In this position we are looking at the block at a true diagonal—that is, from a corner at one side to the extreme corner on the opposite side.

Let us contrast this, and particularly Fig. 142, with the cube which is placed higher up, viewed from the same standpoint.

Flattened Perspective.—Fig. 144 shows the new perspective, in which the three vertical lines (A, A, A) are of equal length, and the six angularly disposed lines (B, C) are of equal length, but shorter than the lines A. The only change which has been made is to shorten the distance across the corner from D to D, but the vertical lines (A) are the same in length as the corresponding lines in Fig. 143. Notwithstanding this change the cubes in both figures appear to be of the same size, as, in fact, they really are.

In forming a perspective, therefore, it would be a good idea for the boy to have a cube of wood always at hand, which, if laid down on a horizontal support, alongside, or within range of the object to be drawn, will serve as a guide to the perspective.

Technical Designations.—As all geometrical lines have designations, I have incorporated such figures as will be most serviceable to the boy, each figure being accompanied by its proper definition.

Before passing to that subject I can better show some of the simple forms by means of suitable diagrams.

Referring to Fig. 145, let us direct our attention to the body (G), formed by the line (D) across the circle. This body is called a segment. A chord (D) and a curve comprise a segment.

Sector and Segment.—Now examine the shape of the body formed by two of the radial lines (E, E) and that part of the circle which extends from one radial line to the other. The body thus formed is a sector, and it is made by two radiating lines and a curved line. Learn to distinguish readily, in your mind, the difference between the two figures.

Terms of Angles.—The relation of the lines to each other, the manner in which they are joined together, and their comparative angles, all have special terms and meanings. Thus, referring to the isometric cube, in Fig. 145, the angle formed at the center by the lines (B, E) is different from the angle formed at the margin by the lines (E, F). The angle formed by B, E is called an exterior angle; and that formed by E, F is an interior angle. If you will draw a line (G) from the center to the circle line, so it intersects it at C, the lines B, D, G form an equilateral or isosceles triangle; if you draw a chord (A) from C to C, the lines H, E, F will form an obtuse triangle, and B, F, H a right-angled triangle.

Circles and Curves.—Circles, and, in fact, all forms of curved work, are the most difficult for beginners. The simplest figure is the circle, which, if it represents a raised surface, is provided with a heavy line on the lower right-hand side, as in Fig. 146; but the proper artistic expression is shown in Fig. 147, in which the lower right-hand side is shaded in rings running only a part of the way around, gradually diminishing in length, and spaced farther and farther apart as you approach the center, thus giving the appearance of a sphere.

Irregular Curves.—But the irregular curves require the most care to form properly. Let us try first the elliptical curve (Fig. 148). The proper thing is, first, to draw a line (A), which is called the "major axis." On this axis we mark for our guidance two points (B, B). With the dividers find a point (C) exactly midway, and draw a cross line (D). This is called the "minor axis." If we choose to do so we may indicate two points (E, E) on the minor axis, which, in this case, for convenience, are so spaced that the distance along the major axis, between B, B, is twice the length across the minor axis (D), along E, E. Now find one-quarter of the distance from B to C, as at F, and with a compass pencil make a half circle (G). If, now, you will set the compass point on the center mark (C), and the pencil point of the compass on B, and measure along the minor axis (D) on both sides of the major axis, you will make two points, as at H. These points are your centers for scribing the long sides of the ellipse. Before proceeding to strike the curved lines (J), draw a diagonal line (K) from H to each marking point (F). Do this on both sides of the major axis, and produce these lines so they cross the curved lines (G). When you ink in your ellipse do not allow the circle pen to cross the lines (K), and you will have a mechanical ellipse.

Ellipses and Ovals.—It is not necessary to measure the centering points (F) at certain specified distances from the intersection of the horizontal and vertical lines. We may take any point along the major axis, as shown, for instance, in Fig. 149. Let B be this point, taken at random. Then describe the half circle (C). We may, also, arbitrarily, take any point, as, for instance, D on the minor axis E, and by drawing the diagonal lines (F) we find marks on the circle (C), which are the meeting lines for the large curve (H), with the small curve (C). In this case we have formed an ovate or an oval form. Experience will soon make perfect in following out these directions.

Focal Points.—The focal point of a circle is its center, and is called the focus. But an ellipse has two focal points, called foci, represented by F, F in Fig. 148, and by B, B in Fig. 149.

A produced line is one which extends out beyond the marking point. Thus in Fig. 148 that part of the line K between F and G represents the produced portion of line K.

Spirals.—There is no more difficult figure to make with a bow or a circle pen than a spiral. In Fig. 150 a horizontal and a vertical line (A, B), respectively, are drawn, and at their intersection a small circle (C) is formed. This now provides for four centering points for the circle pen, on the two lines (A, B). Intermediate these points indicate a second set of marks halfway between the marks on the lines. If you will now set the point of the compass at, say, the mark 3, and the pencil point of the compass at D, and make a curved mark one-eighth of the way around, say, to the radial line (E), then put the point of the compass to 4, and extend the pencil point of the compass so it coincides with the curved line just drawn, and then again make another curve, one-eighth of a complete circle, and so on around the entire circle of marking points, successively, you will produce a spiral, which, although not absolutely accurate, is the nearest approach with a circle pen. To make this neatly requires care and patience.

Perpendicular and Vertical.—A few words now as to terms. The boy is often confused in determining the difference between perpendicular and vertical. There is a pronounced difference. Vertical means up and down. It is on a line in the direction a ball takes when it falls straight toward the center of the earth. The word perpendicular, as usually employed in astronomy, means the same thing, but in geometry, or in drafting, or in its use in the arts it means that a perpendicular line is at right angles to some other line. Suppose you put a square upon a roof so that one leg of the square extends up and down on the roof, and the other leg projects outwardly from the roof. In this case the projecting leg is perpendicular to the roof. Never use the word vertical in this connection.

Signs to Indicate Measurements.—The small circle (°) is always used to designate degree. Thus 10° means ten degrees.

Feet are indicated by the single mark '; and two closely allied marks " are for inches. Thus five feet ten inches should be written 5' 10". A large cross (×) indicates the word "by," and in expressing the term six feet by three feet two inches, it should be written 6' × 3'2".

The foregoing figures give some of the fundamentals necessary to be acquired, and it may be said that if the boy will learn the principles involved in the drawings he will have no difficulty in producing intelligible work; but as this is not a treatise on drawing we cannot go into the more refined phases of the subject.

Definitions.—The following figures show the various geometrical forms and their definitions:

151. Abscissa.—The point in a curve, A, which is referred to by certain lines, such as B, which extend out from an axis, X, or the ordinate line Z. 152. Angle.—The inclosed space near the point where two lines meet. 153. Apothegm.—The perpendicular line A from the center to one side of a regular polygon. It represents the radial line of a polygon the same as the radius represents half the diameter of a circle. 154. Apsides or Apsis.—One of two points, A, A, of an orbit, oval or ellipse farthest from the axis, or the two small dots. 155. Chord.—A right line, as A, uniting the extremities of the arc of a circle or a curve. 156. Convolute (see also Involute).—Usually employed to designate a wave or folds in opposite directions. A double involute. 157. Conic Section.—Having the form of or resembling a cone. Formed by cutting off a cone at any angle. See line A. 158. Conoid.—Anything that has a form resembling that of a cone. 159. Cycloid.—A curve, A, generated by a point, B, in the plane of a circle or wheel, C, when the wheel is rolled along a straight line. 160. Ellipsoid.—A solid, all plane sections of which are ellipses or circles. 161. Epicycloid.—A curve, A, traced by a point, B, in the circumference of a wheel, C, which rolls on the convex side of a fixed circle, D. 162. Evolute.—A curve, A, from which another curve, like B, on each of the inner ends of the lines C is made. D is a spool, and the lines C represent a thread at different positions. The thread has a marker, E, so that when the thread is wound on the spool the marker E makes the evolute line A. 163. Focus.—The center, A, of a circle; also one of the two centering points, B, of an ellipse or an oval. 164. Gnome.—The space included between the boundary lines of two similar parallelograms, the one within the other, with an angle in common. 165. Hyperbola.—A curve, A, formed by the section of a cone. If the cone is cut off vertically on the dotted line, A, the curve is a hyperbola. See Parabola.

Chapter 9, Moldings, With Practical Illustrations in Embellishing Work

Back to Table of Contents