CHAPTER XIofPRACTICAL MECHANICS FOR BOYS
|
The Lever.—The lever is the most wonderful mechanical element in the world. The expression, lever, is not employed in the sense of a stick or a bar which is used against a fulcrum to lift or push something with, but as the type of numerous devices which employ the same principle.
Some of these devices are, the wedge, the screw, the pulley and the inclined plane. In some form or other, one or more of these are used in every piece of mechanism in the world.
Because the lever enables the user to raise or move an object hundreds of times heavier than is possible without it, has led thousands of people to misunderstand its meaning, because it has the appearance, to the ignorant, of being able to manufacture power.
Wrong Inferences from Use of Lever.—This lack of knowledge of first principles, has bred and is now breeding, so-called perpetual motion inventors (?) all over the civilized world. It is surprising how many men, to say nothing of boys, actually believe that power can be made without the expenditure of something which equalizes it
The boy should not be led astray in this particular, and I shall try to make the matter plain by using the simple lever to illustrate the fact that whenever power is exerted some form of energy is expended.
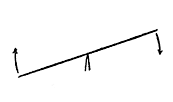
In Fig. 126 is a lever (A), resting on a fulcrum (B), the fulcrum being so placed that the lever is four times longer on one side than on the other. A weight (C) of 4 pounds is placed on the short end, and a 1-pound weight (D), called the power, on the short end. It will thus be seen that the lever is balanced by the two weights, or that the weight and the power are equal.
The Lever Principle.—Now, without stopping to inquire, the boy will say: "Certainly, I can understand that. As the lever is four times longer on one side of the fulcrum than on the other side, it requires only one-fourth of the weight to balance the four pounds. But suppose I push down the lever, at the point where the weight (D) is, then, for every pound I push down I can raise four pounds at C. In that case do I not produce four times the power?"
I answer, yes. But while I produce that power I am losing something which is equal to the power gained. What is that?
First: Look at Fig. 127; the distance traveled. The long end of the lever is at its highest point, which is A; and the short end of the lever is at its lowest point C. When the long end of the lever is pushed down, so it is at B, it moves four times farther than the short end moves upwardly, as the distance from C to D is just one-fourth that from A to B. The energy expended in moving four times the distance balances the power gained.
Power vs. Distance Traveled.—From this the following law is deduced: That whatever is gained in power is lost in the distance traveled.
Second: Using the same figure, supposing it was necessary to raise the short end of the lever, from C to D, in one second of time. In that case the hand pressing down the long end of the lever, would go from A to B in one second of time; or it would go four times as far as the short end, in the same time.
Power vs. Loss in Time.—This means another law: That what is gained in power is lost in time.
Distinguish clearly between these two motions. In the first case the long end of the lever is moved down from A to B in four seconds, and it had to travel four times the distance that the short end moves in going from C to D.
In the second case the long end is moved down, from A to B, in one second of time, and it had to go that distance in one-fourth of the time, so that four times as much energy was expended in the same time to raise the short end from C to D.
Wrongly Directed Energy.—More men have gone astray on the simple question of the power of the lever than on any other subject in mechanics. The writer has known instances where men knew the principles involved in the lever, who would still insist on trying to work out mechanical devices in which pulleys and gearing were involved, without seeming to understand that those mechanical devices are absolutely the same in principle.
This will be made plain by a few illustrations. In Fig. 128, A is a pulley four times larger, diametrically, than B, and C is the pivot on which they turn. The pulleys are, of course, secured to each other. In this case we have the two weights, one of four pounds on the belt, which is on the small pulley (B), and a one-pound weight on the belt from the large pulley (A).
The Lever and the Pulley.—If we should substitute a lever (D) for the pulleys, the similarity to the lever (Fig. 127) would be apparent at once. The pivot (C) in this case would act the same as the pivot (C) in the lever illustration.
In the same manner, and for like reasons, the wedge, the screw and the incline plane, are different structural applications of the principles set forth in the lever.
Whenever two gears are connected together, the lever principle is used, whether they are the same in size, diametrically, or not. If they are the same size then no change in power results; but instead, thereof, a change takes place in the direction of the motion.
 |
 |
| Fig. 129. | Fig. 130. |
| Change of Direction | |
When one end of the lever (A) goes down, the other end goes up, as shown in Fig. 129; and in Fig. 130, when the shaft (C) of one wheel turns in one direction, the shaft of the other wheel turns in the opposite direction.
It is plain that a gear, like a lever, may change direction as well as increase or decrease power. It is the thorough knowledge of these facts, and their application, which enables man to make the wonderful machinery we see on every hand.
Sources of Power.—Power is derived from a variety of sources, but what are called the prime movers are derived from heat, through the various fuels, from water, from the winds and from the tides and waves of the ocean. In the case of water the power depends on the head, or height, of the surface of the water above the discharging orifice.
Water Power.—A column of water an inch square and 28 inches high gives a pressure at the base of one pound; and the pressure at the lower end is equal in all directions. If a tank of water 28 inches high has a single orifice in its bottom 1" x 1" in size, the pressure of water through that opening will be only one pound, and it will be one pound through every other orifice in the bottom of the same size.
Calculating Fuel Energy.—Power from fuels depends upon the expansion of the materials consumed, or upon the fact that heat expands some element, like water, which in turn produces the power. One cubic inch of water, when converted into steam, has a volume equal to one cubic foot, or about 1,700 times increase in bulk.
Advantage is taken of this in steam engine construction. If a cylinder has a piston in it with an area of 100 square inches, and a pipe one inch square supplies steam at 50 pounds pressure, the piston will have 50 pounds pressure on every square inch of its surface, equal to 5,000 pounds.
The Pressure or Head.—In addition to that there will also be 50 pounds pressure on each square inch of the head, as well as on the sides of the cylinder.
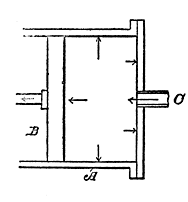
Fig. 131 shows a cylinder (A), a piston (B) and a steam inlet port (C), in which is indicated how the steam pressure acts equally in all directions. As, however, the piston is the only movable part, the force of the steam is directed to that part, and the motion is then transmitted to the crank, and to the shaft of the engine.
 |
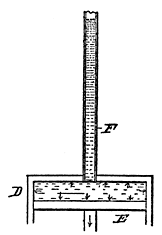 |
| Fig. 131. Steam Pressure | Fig. 132. Water Pressure |
This same thing applies to water which, as stated, is dependent on its head. Fig. 132 represents a cylinder (D) with a vertically movable piston (E) and a standpipe (F). Assuming that the pipe (F) is of sufficient height to give a pressure of 50 pounds to the square inch, then the piston (E) and the sides and head of the cylinder (D) would have 50 pounds pressure on every square inch of surface.
Fuels.—In the use of fuels, such as the volatile hydrocarbons, the direct expansive power of the fuel gases developed, is used to move the piston back and forth. Engines so driven are called Internal Combustion Motors.
Power from Winds.—Another source of power is from the wind acting against wheels which have blades or vanes disposed at such angles that there is a direct conversion of a rectilinear force into circular motion.
In this case power is derived from the force of the moving air and the calculation of energy developed is made by considering the pressure on each square foot of surface. The following table shows the force exerted at different speeds against a flat surface one foot square, held so that the wind strikes it squarely:
| SPEED OF WIND | PRESSURE | SPEED OF WIND | PRESSURE | ||||||||||||
| 5 | Miles | per | hour | 2 | oz. | 35 | miles | per | hour | 6 | lb. | 2 | oz. | ||
| 10 | “ | “ | 88 | “ | 40 | “ | “ | 8 | “ | ||||||
| 15 | “ | “ | 1 | lb. | 2 | “ | 45 | “ | “ | 10 | “ | 2 | “ | ||
| 20 | “ | “ | 2 | “ | “ | 50 | “ | “ | 12 | “ | 2 | “ | |||
| 25 | “ | “ | 3 | “ | 2 | “ | 55 | “ | “ | 15 | “ | 2 | “ | ||
| 30 | “ | “ | 4 | “ | 8 | “ | 60 | “ | “ | 18 | “ | ||||
Varying Degrees of Pressure.—It is curious to notice how the increase in speed changes the pressure against the blade. Thus, a wind blowing 20 miles an hour shows 2 pounds pressure; whereas a wind twice that velocity, or 40 miles an hour, shows a pressure of 8 pounds, which is four times greater than at 20 miles.
It differs, therefore, from the law with respect to water pressure, which is constant in relation to the height or the head—that is, for every 28 inches height of water a pound pressure is added.
Power from Waves and Tides.—Many attempts have been made to harness the waves and the tide and some of them have been successful. This effort has been directed to the work of converting the oscillations of the waves into a rotary motion, and also to take advantage of the to-and-fro movement of the tidal flow. There is a great field in this direction for the ingenious boy.
A Profitable Field.—In no direction of human enterprise is there such a wide and profitable field for work, as in the generation of power. It is constantly growing in prominence, and calls for the exercise of the skill of the engineer and the ingenuity of the mechanic. Efficiency and economy are the two great watchwords, and this is what the world is striving for. Success will come to him who can contribute to it in the smallest degree.
Capital is not looking for men who can cheapen the production of an article 50 per cent., but 1 per cent. The commercial world does not expect an article to be 100 per cent, better. Five per cent. would be an inducement for business.
To Table of Contents and Glossary